Berechnung Cyclogetriebe ?

[Geistesblitz]

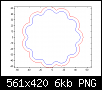
Da mich das Thema sowieso schon ein bisschen interessiert hat, hab ich mal versucht eine Formel für den Kram zu finden und hab sogar etwas herausbekommen. Kannst du mit Matlab etwas anfangen? Hier das, was ich geschrieben habe:

clear all;
close all;
clc;

n=12;       % Anzahl Wälzzylinder
e=3;        % Exzentrizität
r=5;        % Radius der Wälzzylinder
R=50;       % Radius der Scheibe
phi=0:0.01:2*pi;

for i=1:size(phi,2)
    x(i)=R*cos(phi(i))+e*cos(n*phi(i));
    y(i)=R*sin(phi(i))+e*sin(n*phi(i));
    absr=sqrt(R^2+(n*e)^2+2*R*n*e*(cos(phi(i))*cos(n*phi(i))+sin(phi(i))*sin(n*phi(i))));
    x_zyk(i)=x(i)-(R*cos(phi(i))+e*n*cos(n*phi(i)))*r/absr;
    y_zyk(i)=y(i)-(R*sin(phi(i))+e*n*sin(n*phi(i)))*r/absr;
end

figure;
plot(x,y,'r',x_zyk,y_zyk,'b');
axis equal;

Ergebnis sieht dann so aus (blaue Linie: Außenkontur der Scheibe, rote Linie: Bahn der Wälzzylinderachsen):